부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다.

Basic

유저는 직접 검색을 하지 않아도, 추천 알고리즘에 따라 유저의 취향에 맞는 아이템을 추천 받는다. (1) 유저의 직접적인 가이드가 없는 상황에서도 아이템을 선별해 주는 것과, (2) 다양한 아이템을 추천해 주는 것(long tail recommendation)이 추천 시스템의 핵심이다.

데이터

유저 정보
- 유저 프로파일링, 식별자, 유저 행동 정보 등
아이템 정보
- 아이템 고유 정보
유저 - 아이템 상호작용 정보
- explicit feedback: 별점과 같은 직접적인 선호 정보
- implicit feedback: 클릭 로그, 구매 이력 등 간접적인 선호 정보

문제 정의

Ranking
- 유저에게 적합한 아이템 K개를 추천하는 문제
- 유저의 아이템들 간 선호 순서를 학습
- Precision@K, Recall@K, MAP@K, nDCG@K
Prediction
- 유저가 아이템에 가질 선호도를 정확하게 예측하는 문제
- 평점 예측, 구매할 확률 예측 등.
- MAE, RMSE, AUC 등으로 평가

Evaluation Metric

추천 모델을 가장 쉽게 평가하는 방법은 offline 평가이다. 데이터셋을 Train, Valid, Test로 나눠 수치적으로 모델의 성능을 평가한다. offline 평가의 성능이 좋다고 항상 online 성능이 보장되는 것은 아니지만, 모델을 배포하기 전에 평가가 가능하다는 이점이 있어 사전 검증용으로 쓰인다.

Precision@K

추천한 K개의 아이템 가운데 실제 유저가 관심있는 아이템의 비율

Recall@K

유저가 관심있는 전체 아이템 가운데 추천한 아이템의 비율

AP@K

$AP@K = \frac{1}{m}\sum_{i=1}^K Precision@i$

Precision@1부터, Precision@K까지의 평균값

관련 아이템을 더 높은 순위에 추천할수록 점수가 높아진다.

MAP@K

$MAP@K = \frac{1}{|U|}\sum_{u=1}^{|U|}(AP@K)_u$

모든 유저에 대한 AP값의 평균

nDCG

Cumulative Gain (CG): 상위 K개 아이템에 대하여 관련도를 합한 것

$CG_k = \sum_{i=1}^K rel_i$
Discounted Cumulative Gain (DCG): 순서에 따라 가중치 부여

$DCG_k = \sum_{i=1}^K \frac{rel_i}{log_2(i+1)}$
Ideal DCG (IDCG): Ideal한 DCG

$IDCG = \sum_{i=1}^K \frac{rel_i^{opt}}{log_2(i+1)}$
Normalized DCG (NDCG): 추천 결과에 따른 DCG를 IDCG로 나눈 값

$NDCG = \frac{DCG}{IDCG}$

Collaborating filtering

많은 유저들로부터 얻은 기호 정보를 이용해 유저의 관심사를 예측하는 방법

목표

유저 u가 아이템 i에 부여할 평점을 예측하는 것

방법

유저-아이템 행렬 생성
유저, 아이템 간 유사도 계산
나머지 비어있는 부분 채우기

Neighborhood-based CF

Memory-based CF라고도 한다.

특징

구현이 간단
새로운 아이템, 유저에 대한 낮은 확장성
sparsity ratio가 99.5%를 넘으면 성능이 떨어짐 -> 넘을 경우 Matrix Factorization 추천

K-Nearest Neighbors CF (KNN CF)

NBCF의 모든 관계를 학습해야 하는 단점을 극복
유저 u와 가장 유사한 K명의 유저를 이용해 평점 예측(K 값은 보통 25 ~ 50 사이값으로 튜닝)

유사도 측정법

Mean Squared Difference Similarity
- 유클리드 거리에 반비례
Cosine Similarity
- 두 벡터가 가르키는 방향의 유사도(크기는 무시됨)
Pearson Similarity (Pearson Correlation)
- 각 벡터를 표본평균으로 정규화한 뒤에 코사인 유사도를 구한 값(유저마다 평점을 주는 분포가 다르기 때문)
- 직관적인 해석: (X와 Y가 함께 변하는 정도) / (X와 Y가 따로 변하는 정도)
Jaccard Similarity
- 주어진 두 집합 A, B에 대해 계산
- 벡터가 아니기 때문에, 서로 길이가 달라도 됨.
- 두 집합이 얼마나 같은 아이템을 공유하고 있는지 나타냄.
- 두 집합이 가진 아이템이 모두 같으면 1, 하나도 없으면 0

유사도 측정 방법은 오프라인 테스트를 통한 성능을 근거로 결정할 수 있다.

Model Based Collaborative Filtering

항목 간 유사성을 단순 비교하는 것에서 벗어나 데이터에 내재한 패턴을 이용해 추천하는 방법

NBCF의 한계

sparsity
scalability

해결 방법

Parametric Machine Learning을 사용, 데이터 정보가 파라미터의 형태로 모델에 압축
유저-아이템 데이터는 학습에만 사용되고 학습된 모델은 압축된 형태로 저장됨
limited coverage 극복

Latent Factor Model

유저와 아이템을 저차원의 행렬로 분해, 유저와 가까운 위치의 아이템을 추천

Singular Value Decomposition (SVD)

Item-User Rating Matrix를 분해
한계: 결측된 entry를 모두 채우는 imputation을 통해 Dense Matrix를 만들어 SVM를 수행 즉, 빈 칸을 0 또는 유저, 아이템 평균 평점으로 채움 → 기존 데이터가 왜곡되기 쉬움.
전체 factor를 쓰는 Full SVD와 일부 factor를 쓰는 Truncated SVD가 있음.

Matrix Factorization

SVD와 유사하지만, 관측된 데이터만 활용하여 Rating Matrix를 잠재 요인의 행렬 곱으로 근사하자.

$\hat{R} = P \times Q^T$

objective function

$min_{P,Q}\sum_{observed r_{u,i}}(r_{u,i}-p_u^Tq_i)^2 + \lambda(\lVert p_u \rVert ^2_2 + \lVert q_i \rVert ^2_2)$

실제 관측값과, latent vector의 곱이 가까워지도록 학습하는 term + vector에 대한 L2 정규화 term

학습

SGD
$\frac{\partial L}{\partial p_u} = \frac{\partial (r_{ui} - p_u^T q_i)^2}{\partial p_u} + \frac{\partial \lambda \lVert p_u \rVert_2^2}{\partial p_u} = -2(r_{ui} - p_u^T q_i) q_i + 2 \lambda p_u = -2(e_{ui} q_i - \lambda p_u)$
Gradient의 반대방향으로 $p_u$ , $q_i$ 를 업데이트
$p_u \leftarrow p_u + \eta \cdot (e_{ui} q_i - \lambda p_u)$ $q_i \leftarrow q_i + \eta \cdot (e_{ui} p_u - \lambda q_i)$
ALS
- 행렬(P)과 아이템 행렬(Q)을 번갈아 고정하고, 고정한 상태에서 다른 하나를 Least Squares 방식으로 해결
- 새로운 objective function
  $\min_{P, Q} \sum_{\text{observed } f_{u,i}} c_{u,i} (f_{u,i} - p_u^T q_i)^2 + \lambda \left( \sum_u \lVert p_u \rVert_2^2 + \sum_i \lVert q_i \rVert_2^2 \right)$ $p_u = (Q^TQ + \lambda I)^{-1}Q^Tr_u$ $q_i = (P^TP + \lambda I)^{-1}P^Tr_i$

추가 개선

Matrix Factorization Techniques for Recommender Systems

Adding Biases: 개별 유저와 아이템에 대한 편향 b를 학습함
Adding Confidence Level: 데이터의 신뢰도를 의미하는 c 파라미터를 추가
Adding Temporal Dynamics: Adding Temporal Dynamics

Neural Matrix Factorization

기존 Matrix Factorization에 MLP를 추가하여, user-item의 복잡한 관계를 학습

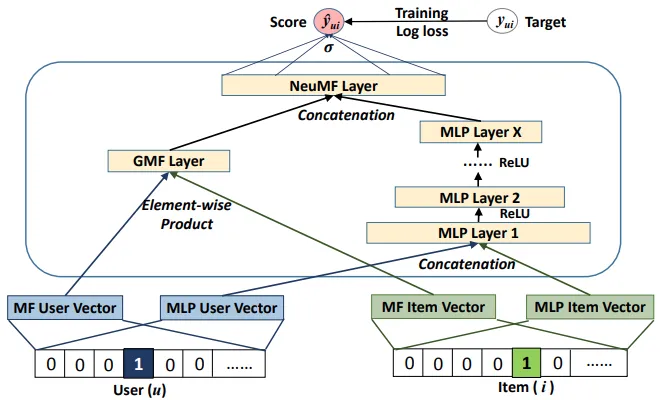
Neural_MF

출처: Neural Collaborative Filtering

Bayesian Personalized Ranking (BPR)

사용자에게 순서가 있는 아이템 리스트를 제공하는 문제
유저의 아이템에 대한 선호 순위를 Matrix Factorization 학습에 반영

BPR: Bayesian Personalized Ranking from Implicit Feedback

가정

관측된 item을 관측되지 않은 item보다 선호
관측된 것들 사이에 선호도 추론 불가
관측되지 않은 것들 사이에 선호도 추론 불가

특징

관측되지 않은 아이템도 학습함
관측되지 않은 아이템 간에도 ranking이 가능

최대 사후 확률 추정(Maximum A Posterior, MAP)

주어진 유저 선호 정보를 최대한 잘 나타내는 파라미터를 추정

모든 유저 선호 정보( $>_u$ ) 에 대한 likelihood:
$\prod_{u \in U} p(>_u \mid \Theta) = \prod_{(u, i, j) \in \mathcal{D}_S} p(i >_u j) = \prod_{(u, i, j) \in \mathcal{D}_S} \sigma \left( \hat{x}_{uij}(\Theta) \right)$ $\hat{r}_{ui} = p_u^T q_i, \quad \hat{r}_{uj} = p_u^T q_j$ $\hat{x}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} = p_u^T q_i - p_u^T q_j$ $p(i >_u j) := \sigma \left( \hat{x}_{uij}(\Theta) \right), \quad \sigma(x) := \frac{1}{1 + e^{-x}} \quad \text{(sigmoid function)}$
objective function
$\begin{align} \text{BPR-OPT} := \ln p(\Theta \mid >_u) &= \ln p(>_u \mid \Theta) \cdot p(\Theta) \\ &= \ln \prod_{(u, i, j) \in \mathcal{D}_S} \sigma(\hat{x}_{uij}) \cdot p(\Theta) \\ &= \sum_{(u, i, j) \in \mathcal{D}_S} \ln \sigma(\hat{x}_{uij}) + \ln p(\Theta) \\ &= \sum_{(u, i, j) \in \mathcal{D}_S} \ln \sigma(\hat{x}_{uij}) - \lambda_\Theta \lVert \Theta \rVert^2 \\ \end{align}$

항목	Memory-based	Model-based
Training and Inference Complexity	- Training 필요 없음 Inference를 위해서 많은 양의 Offline 계산(similar-item tables을 만드는 작업)이 요구됨	- 모델 학습을 위해 값비싼 offline training이 요구됨 한 번 학습된 후에는 비교적 빠르게 inference 가능함
Interpretability	- Interaction 데이터 기반의 similarity를 계산하여 활용하기 때문에 추천의 이유에 대해 직관적인 설명을 제공함	- Parametric 모델의 특성 상 black-box인 측면이 있음
Accuracy	- 직접적으로 accuracy 메트릭을 최적화하지 않으므로 불리함 (휴리스틱 방법의 한계)	- MSE 등의 objective function을 직접적으로 최적화하므로 유리함

Item2Vec

Embedding: 주어진 데이터를 낮은 차원의 벡터로 표현하는 방법이다. 벡터 공간 상에서 의미 기반의 연산이 가능해진다. 추천 시스템에서는 유저와 아이템을 벡터로 나타내고, 이 벡터들 간의 유사도를 기반으로 추천을 수행한다.

Sparse Representation

one-hot encoding, multi-hot encoding처럼 전체 feature 공간에 걸쳐 희소하게 표현됨
차원이 높고 연산이 비효율적

Dense Representation

비교적 작은 차원에 정보를 압축하여 표현
연산 효율성과 의미 표현력이 높음
추천 시스템의 핵심 표현 방식

대량의 코퍼스에서 학습
의미를 내포한 벡터 표현
연산 효율이 높고 빠르게 학습 가능
유사한 단어는 벡터 공간 상에서 가까운 위치

학습 방법

CBOW (Continuous Bag of Words)
- 주변 단어들을 이용해 중심 단어를 예측
- 전체 문맥의 평균을 통해 예측
Skip-Gram
- 중심 단어로 주변 단어들을 예측
- 일반적으로 CBOW보다 성능이 더 좋음
Skip-Gram with Negative Sampling (SGNS)
- 실제 단어쌍은 label 1, 무작위 단어쌍은 label 0으로 binary classification
- 하나의 positive sample마다 여러 negative sample 생성
- 효율적으로 대규모 데이터셋 학습 가능