부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다.

AutoEncoder for Recommender Systems

입력 데이터를 출력으로 복원하는 비지도 학습 모델.
중간 hidden layer는 input 데이터의 feature representation으로 활용된다.
이상치 탐지, 표현 학습, 이미지 노이즈 제거 등 다양한 활용 가능.

AutoEncoder

• 기본 구조

  • 입력 데이터를 압축된 표현(latent vector)으로 인코딩 → 다시 복원
  • reconstruction error를 최소화하며 학습

• Denoising AutoEncoder

  • 입력에 noise(dropout 등)를 추가해도 원래 데이터를 잘 복원하도록 학습
  • 더 robust한 표현 학습 가능

AutoRec

AutoEncoder 구조를 추천 시스템의 행렬 완성(Matrix Completion) 문제에 적용

AutoRec: Autoencoders Meet Collaborative Filtering

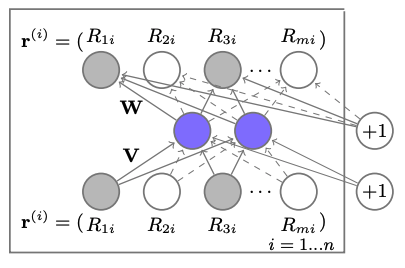
• 문제 상황

  • rating vector에 관측되지 않은 값이 존재
  • AutoEncoder를 통해 유저 or 아이템 벡터를 latent feature로 표현 → 평점 예측에 활용 가능

• 구조

  • 유저 기반 AutoRec: 아이템 rating vector를 입력
  • 아이템 기반 AutoRec: 유저 rating vector를 입력
    → 둘 중 하나만 임베딩하고, 나머지는 고정된 값으로 사용

• 수식

  • 목표: 기존 rating과 재구성된 rating의 차이(RMSE)를 최소화
  $$\min_{\theta} \sum_{r \in S} \| r - h(r;\theta) \|^2_2$$ $$h(r; \theta) = f \left( W \cdot g(Vr + \mu) + b \right)$$
  • 비선형 함수 f, g 사용 가능 (예: sigmoid, identity)

CDAE (Collaborative Denoising AutoEncoder)

Denoising AutoEncoder를 활용한 Top-N 추천에 최적화된 모델

Collaborative Denoising Auto-Encoders for Top-N Recommender Systems

• 입력

  • 유저-아이템 상호작용 정보를 (0,1) preference 값으로 변환
  • 랜덤하게 일부 아이템을 제거(dropout처럼) → 복원 학습
  • 유저 임베딩($V_u$)을 함께 학습하여 personalization 강화

• 확률적 입력 생성

  • 유저 u가 아이템 i를 선호함:

    $P(\tilde{y}_{ui} = \delta_{yu}) = 1 - q$

    $P(\tilde{y}_{ui} = 0) = q$

• 디코딩 방식

  • 인코더 출력($z_u$)을 기반으로 아이템별 예측 수행
  $$z_u = h(W^T \tilde{y}_u + V_u + b)$$ $$\hat{y}_{u,i} = f(W_i^T z_u + b'_i)$$

• 목표

  • 노이즈가 있는 입력에서 원래의 선호 벡터를 재구성 → Top-N 추천을 위한 score 생성

Recommender System with GNN

그래프는 관계와 상호작용 같은 추상적인 개념을 표현하기에 적합하다. 추천 시스템에서도 유저-아이템 간의 상호작용을 그래프 형태로 모델링하면 효과적인 임베딩 학습이 가능하다.

GNN (Graph Neural Network)

• 목표: 주변 이웃 노드 정보를 종합해 중심 노드의 표현(임베딩)을 학습
• 방법: 인접 행렬 + 피처 행렬을 입력으로 하여 MLP 적용
• 한계:
  • 노드 수가 많아질수록 연산량 급증($N^2$)
  • 인접행렬의 순서는 실제 graph와 아무 관계가 없지만, 노드의 순서가 바뀌면 의미가 달라짐

GCN (Graph Convolutional Network)

• 목표: Convolution 구조를 통해 연산 효율성과 지역적 특징 학습
• 특징:
  • local connectivity
  • shared weights (필터 역할)
  • multi-layer 구조로 high-order 관계까지 포착

1. Neural Graph Collaborative Filtering (NGCF)

유저-아이템 상호작용을 그래프 구조로 표현하고, GNN 기반 message passing을 통해 고차원의 관계까지 포착하는 추천 모델

Neural Graph Collaborative Filtering

문제 상황

• 기존 CF 모델은 유저와 아이템 임베딩만 사용해 상호작용을 직접적으로 반영하지 못함
• 상호작용 학습이 임베딩과 분리되어 sub-optimal한 결과를 초래할 수 있음

→ 상호작용 자체를 임베딩 단계에서 학습해야 함

핵심 아이디어

• Collaborative Signal을 임베딩 단계에서 학습
• GNN 구조를 통해 high-order 이웃 관계를 반영

모델 구조

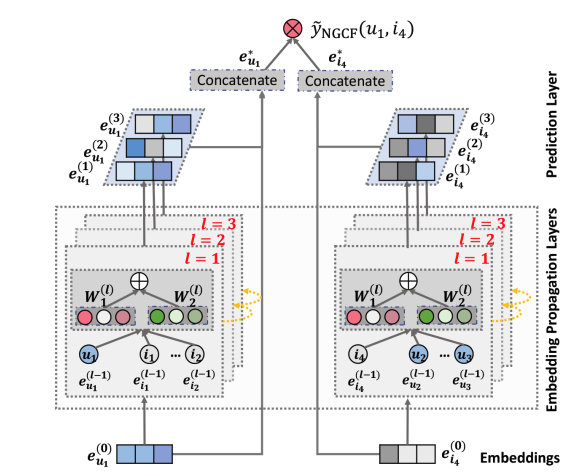
임베딩 레이어

• 유저와 아이템의 초기 임베딩 제공
• 기존 CF 모델과 달리, interaction function에 직접 넣지 않고 전파 레이어로 전달하여 학습
• 전체 임베딩 행렬($\mathbf{E}$):

임베딩 전파 레이어 (Embedding Propagation Layer)

High-order connectivity 학습

• First-order Propagation

  • Message Construction**
    유저-아이템 간 affinity를 고려하여 메시지를 구성
  $$\mathbf{m}_{u \leftarrow i} = \frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}} \left( \mathbf{W}_1 \mathbf{e}_i + \mathbf{W}_2 (\mathbf{e}_i \odot \mathbf{e}_u) \right)$$

  • $\odot$: element-wise product

  • $\mathbf{W}_1, \mathbf{W}_2$: 학습 가능한 weight matrix

  • Message Aggregation**

  $$\mathbf{e}_u^{(1)} = \text{LeakyReLU} \left( \mathbf{m}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_u} \mathbf{m}_{u \leftarrow i} \right)$$

  → 1-hop 이웃의 메시지를 종합하여 유저 임베딩 갱신

• Higher-order Propagation

  계층적으로 l-hop 이웃까지 전파

  $$\mathbf{e}_u^{(l)} = \text{LeakyReLU} \left( \mathbf{m}^{(l)}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_u} \mathbf{m}^{(l)}_{u \leftarrow i} \right)$$

  메시지 구성:

  $$\mathbf{m}^{(l)}_{u \leftarrow i} = p_{ui} \left( \mathbf{W}_1^{(l)} \mathbf{e}_i^{(l-1)} + \mathbf{W}_2^{(l)} ( \mathbf{e}_i^{(l-1)} \odot \mathbf{e}_u^{(l-1)} ) \right)$$

선호도 예측 레이어 (Prediction Layer)

• 각 propagation layer의 임베딩을 concat하여 최종 임베딩 계산

• 예측은 단순한 내적으로 계산

특징

• GNN을 통해 유저-아이템 임베딩을 더 명확하게 분리 가능
• L=3~4일 때 가장 좋은 성능 보임
• MF보다 높은 Recall 및 표현력 확보

2. LightGCN

LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation

핵심 아이디어

• GCN에서 불필요한 non-linear 연산, weight matrix 제거
• 핵심적인 message passing 구조만 유지
• 파라미터 수와 연산량 감소

구조 요약

• self-connection 제거
• non-linear activation 제거
• 각 layer 임베딩의 weighted average 사용

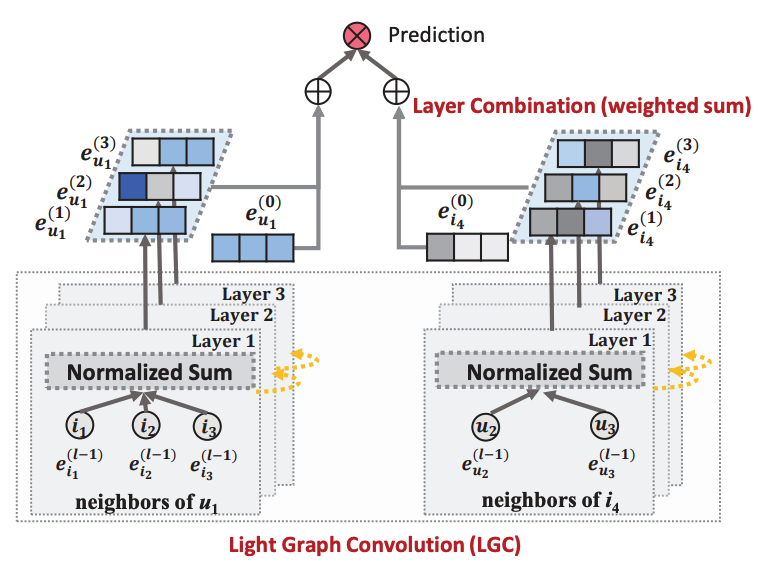
수식

• 임베딩 전파

• 최종 임베딩 계산

• 선호도 예측

Context-aware Recommendation

상호작용이 없는 유저에 대해서는 CF 기반의 추천이 어려움. 따라서 맥락 정보를 활용하자.

활용 예시: CTR 예측

• Logistic Regression

  • $logit(P(y=1 \mid x)) = (w_0 + \sum_{i=1}^n w_ix_i)$ .
  • 상호작용을 반영하지 않음

• polynomial model

  • $logit(P(y=1 \mid x)) = (w_0 + \sum_{i=1}^n w_ix_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij}x_ix_j)$ .
  • 변수 간 상호작용을 고려, 파라미터 수가 급격히 증가함

• CTR 예측 문제에서 사용되는 데이터는 대부분 Sparse함(대부분 category 변수)

  • 파라미터 수가 너무 많아짐

• one-hot encoding의 한계

  • 해결책: 피쳐 임베딩을 한 후, 피쳐로 사용

Factorization Machine (FM)

Factorization Machines

문제 상황

• 기존 머신러닝 모델(SVM 등)은 sparse한 데이터에 약함
• MF는 추천 성능은 좋지만, 일반화가 어렵고 유저-아이템 데이터 전용

→ SVM과 MF의 장점을 결합한 모델이 필요

모델 구조

FM은 이차 상호작용 항을 효율적으로 모델링할 수 있는 구조이다.

• $w_0$: bias term
• $w_i$: 1차 선형 weight
• $\langle v_i, v_j \rangle$: 임베딩 벡터 간 내적 (2차 상호작용 표현)
• $v_i \in \mathbb{R}^k$: i번째 feature의 임베딩

상호작용이 sparse한 상황에서도 내적 구조로 일반화된 표현 학습이 가능하다

Example

• 입력: 유저-아이템-평점 데이터
  $(user_1, movie_2, 5), (user_3, movie_1, 4), \dots$

• 영화에 대한 벡터: 다양한 유저의 평점으로 학습됨

• 유저에 대한 벡터: 유저가 본 영화들로부터 간접적으로 학습됨

Field-aware Factorization Machine (FFM)

FM 구조에서, 피처가 다른 필드(field)와 상호작용할 때마다 별도의 임베딩 벡터를 사용

Pairwise interaction tensor factorization for personalized tag recommendation

Field-aware Factorization Machines for CTR Prediction

모델 구조

FFM은 feature를 field 단위로 나누고, 상호작용 시 해당 field에 맞는 embedding vector를 사용함

• $v_{i, f_j}$: feature $i$가 field $j$와 상호작용할 때의 임베딩
• $f$: field의 개수 → 파라미터 수는 $O(n \cdot f \cdot k)$

CTR Prediction

Wide & Deep

Google에서 App recommendation을 위해 제안한 모델로, memorization과 generalization을 동시에 해결할 수 있도록 설계

Wide & Deep Learning for Recommender Systems

모델 구조

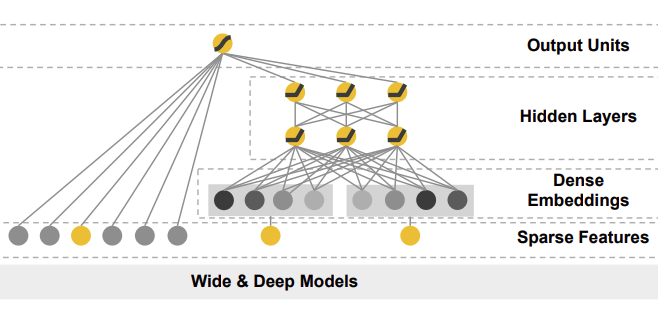
Wide Component

기본적인 선형 모델 구조.
변수들 간의 직접적인 상호작용을 반영하기 위해 cross-product transformation을 사용한다.

• 입력 feature: $\mathbf{x}$

• 예측 함수:
  $\hat{y}_{\text{wide}} = \mathbf{w}^\top [\mathbf{x}, \phi(\mathbf{x})] + b$
  $\phi(\mathbf{x})$는 cross-feature transformation (e.g. $x_i \cdot x_j$)

• 모든 조합에 대해 cross-product를 적용하면 파라미터 수가 너무 많아지므로, 일반적으로 중요한 feature들에만 2차 interaction을 적용

Deep Component

Feedforward Neural Network 구조.

• 연속형 변수는 그대로 사용
• 범주형 변수는 one-hot, embedding vector로 변환 후 입력
• 3 layer, ReLU 함수 사용

예측 함수:

DNN의 최종 출력은 wide component와 결합하여 사용된다.

Final Prediction

두 컴포넌트의 결과를 합쳐 최종 예측 값을 생성한다:

DeepFM

FM 기반의 Neural Network 모델

DeepFM: A Factorization-Machine based Neural Network for CTR Prediction

• 기존 Wide & Deep 모델과 달리, 두 컴포넌트(Wide, Deep)가 입력값을 공유하며, end-to-end 방식으로 학습된다.
• 즉, 별도의 feature engineering (cross-product 등)이 필요 없다.

등장 배경

• 추천 시스템에서는 **암묵적인 feature interaction(implicit interaction)**을 학습하는 것이 중요하다.
• 기존 모델들은 low-order interaction 또는 high-order interaction 중 하나만 다룬다.
• Wide & Deep 모델은 이를 해결하였지만, Wide component는 여전히 feature engineering이 필요하다.

→ FM을 wide component로 사용하고, 입력값을 공유하도록 개선한 것이 DeepFM

모델 구조

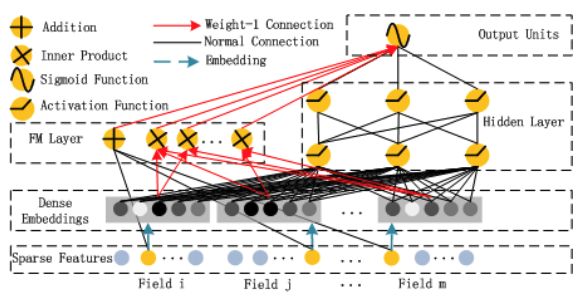
• FM Component (Wide)

  기존 Factorization Machine과 동일한 구조로, 2차 상호작용을 모델링

  $$\hat{y}_{FM} = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j$$
  • $\langle v_i, v_j \rangle$: feature 간 내적
  • $v_i$: field i에 대한 임베딩

  → low-order interaction을 효과적으로 포착

• Deep Component

  모든 feature를 동일한 차원의 embedding vector로 변환한 후, DNN에 입력

  • DNN 구조:
  $$a^0 = [e_1, e_2, \dots, e_m]$$ $$a^{(l+1)} = \sigma(W^{(l)} a^{(l)} + b^{(l)})$$ $$\hat{y}_{DNN} = W^{(L)} a^{(L)} + b^{(L)}$$
  • $e_i$: feature $x_i$의 embedding
  • $\sigma$: 활성화 함수 (ReLU, sigmoid 등)
  • high-order feature interaction을 학습

  임베딩 값은 FM과 공유됨 (공통의 $v_i$ 사용)

• 전체 구조

  최종 예측값은 FM component와 DNN component의 출력을 더한 후, sigmoid를 적용

  $$\hat{y} = \sigma(\hat{y}_{FM} + \hat{y}_{DNN})$$

Deep Interest Network (DIN)

현재 예측하려는 아이템이 과거 소비 아이템과 얼마나 연관성이 있는가

Deep Interest Network for Click-Through Rate Prediction

기존의 딥러닝 기반 추천 모델들은 대부분 embedding → MLP 형태를 따르며, 고정된 길이의 입력으로만 유저의 선호를 표현한다. DIN은 가변적인 길이의 행동 이력을 가중합을 통해 예측에 반영한다.

하지만 실제 유저는 다양한 관심사를 동시에 가질 수 있다. DIN은 이러한 user behavior의 다양성을 반영한다.

모델 구조

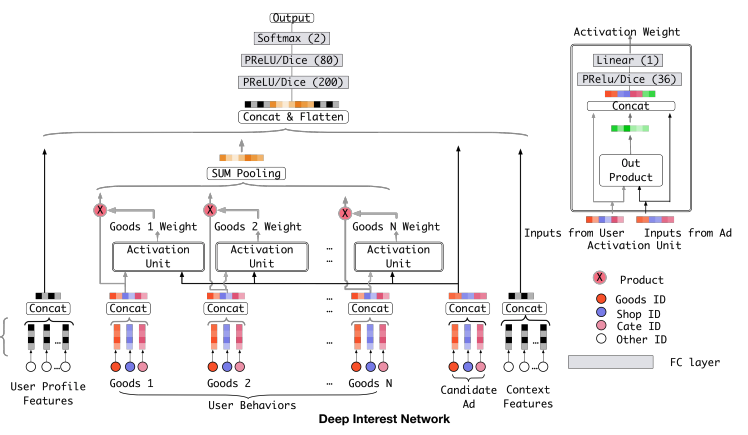
• Embedding Layer

  • user profile, context, candidate ad 등 모든 입력 feature를 embedding vector로 변환
  • user behavior sequence는 multi-hot encoding → embedding → sequence vector

• Local Activation Layer

  user behavior sequence 내에서 타겟 아이템과 관련된 과거 항목을 강조하기 위한 모듈

• Local Activation Unit

  • 각 과거 아이템과 target 아이템의 연관성 정도를 계산하여 weight 부여
  • 구조적으로는 attention mechanism과 유사
  • 연산 방식:
  $$a_i = \text{ActivationUnit}(e_i, e_{target})$$
  • 각 $e_i$는 과거 행동 아이템의 embedding, $e_{target}$은 현재 예측할 아이템의 embedding

• Weighted Sum Pooling

  • 위에서 계산된 weight를 기반으로 user behavior representation vector 생성
  $$v_u = \sum_{i=1}^n a_i \cdot e_i$$
  • 과거 행동 벡터들의 weighted 평균으로 유저의 현재 관심 표현

• Fully-connected Layer

  • 위에서 만든 user behavior representation, user profile, target ad 등을 concat
  • 일반적인 MLP를 거쳐 예측값 계산
  $$\hat{y} = \text{MLP}([\text{user profile}, v_u, \text{ad features}])$$

Behavior Sequence Transformer (BST)

NLP 문제와의 유사성을 기반으로 Transformer의 구조를 추천에 적용

Behavior Sequence Transformer for E-commerce Recommendation in Alibaba

• CTR 예측 데이터와 NLP 데이터 간의 공통점

  • 대부분 sparse feature로 구성됨
  • low-order, high-order feature interaction 모두 존재
  • 순서 정보가 중요

  → User Behavior Sequence를 순서 있는 시퀀스로 취급하고, Transformer의 인코더 레이어만 사용한다.

모델 구조

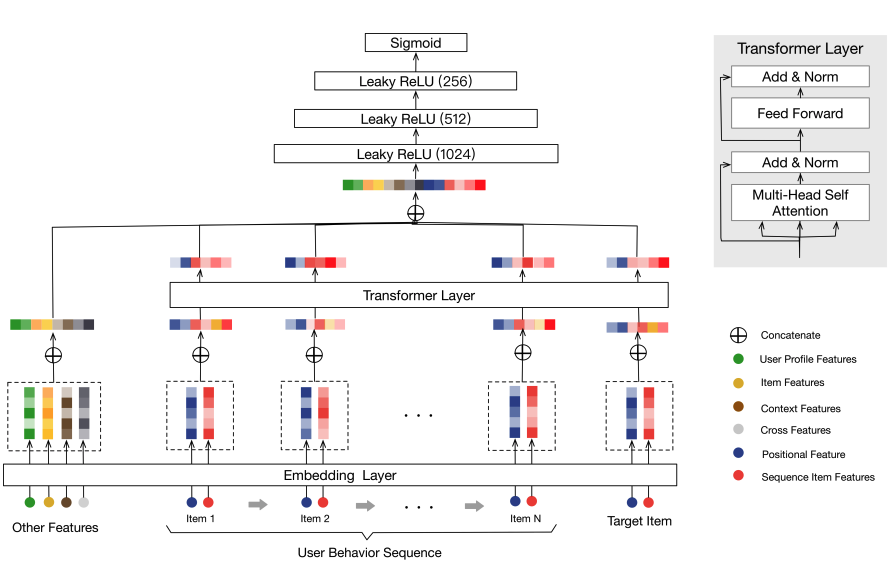
입력 구성

• Other Features: user profile, context 등

• User Behavior Sequence: 과거 소비한 아이템 시퀀스

• Target Item: 예측 대상 아이템

• Positional Encoding: 순서를 표현하기 위해 사용됨

  $$pos(v_i) = t(v_t) - t(v_i)$$
  • 현재 시간 $t(v_t)$ 과 과거 아이템 소비 시간 $t(v_i)$의 차이를 기반으로 함 (absolute time이 아닌 상대 시간 기반)

Transformer Encoder Layer

$S = \text{MultiHead-Attention}(E)$

$F = \text{FFN}(S)$

정규화 및 드롭아웃까지 포함한 수식:

→ 이를 여러 레이어 반복 (1~4개 사용 가능)

MLP 후 처리

Transformer에서 나온 출력 벡터와 user profile, context, target item 등을 concat한 후, MLP에 통과시켜 예측값 산출