추천 시스템 정리 (3)
2025년 04월 14일
#AI
소개기록서랍

부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다.

Bandit for Recommendation

Multi-Armed Bandit(MAB) 문제는 강화학습의 기초적인 형태로, 여러 개의 슬롯머신(arm)이 존재할 때 어떤 arm을 어떤 순서로 선택할 것인가에 대한 문제이다. 각 arm은 서로 다른 확률분포로 reward를 생성힌다.

Deep Bayesian Bandits: Exploring in Online Personalized Recommendations

  • Exploration (탐색): 다양한 arm을 시도하며 reward 정보를 수집
  • Exploitation (활용): 현재까지의 관측 정보를 바탕으로 가장 좋아 보이는 arm을 선택

이 둘 사이의 trade-off를 조절

Greedy Algorithm (Simple Average Method)

가장 간단한 방법으로, 평균 reward가 가장 높은 action을 선택

Qt(a)=∑i=1t−1Ri⋅1Ai=a∑i=1t−11Ai=aQ_t(a) = \frac{\sum_{i=1}^{t-1} R_i \cdot \mathbb{1}_{A_i=a}}{\sum_{i=1}^{t-1} \mathbb{1}_{A_i=a}}
  • 문제: 초기 선택에 따라 특정 action에 bias가 생김 → exploration 부족

Epsilon-Greedy Algorithm

  • 확률적으로 exploration을 추가
At={arg⁡max⁡aQt(a),with probability 1−ϵrandom action,with probability ϵA_t = \begin{cases} \arg\max_a Q_t(a), & \text{with probability } 1 - \epsilon \\ \text{random action}, & \text{with probability } \epsilon \end{cases}
  • 간단하면서도 강력한 성능을 보임

Upper Confidence Bound (UCB)

  • 각 action에 대해 **uncertainty(불확실성)**을 고려해 선택
  • 적게 선택된 arm에는 더 높은 exploration 보상을 부여
At=arg⁡max⁡a[Qt(a)+cln⁡tNt(a)]A_t = \arg\max_a \left[ Q_t(a) + c \sqrt{ \frac{\ln t}{N_t(a)} } \right]
  • Nt(a)N_t(a): action a가 선택된 횟수
  • cc: 탐색 계수 (하이퍼파라미터)

Thompson Sampling

ThompsonSampling

A Tutorial on Thompson Sampling

  • 각 action의 reward를 확률분포(베타분포)로 모델링하고, 샘플링된 확률값이 가장 높은 arm 선택
Beta(x∣α,β)=1B(α,β)xα−1(1−x)β−1\text{Beta}(x|\alpha, \beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1}
  1. 각 arm의 초기 prior: Beta(1,1)\text{Beta}(1,1)
  2. 클릭: α←α+1\alpha \gets \alpha + 1, 클릭 안함: β←β+1\beta \gets \beta + 1
  3. posterior로부터 샘플링하여 가장 높은 값을 선택
  • 장점: 베이지안 방식, natural한 exploration 제공

LinUCB (Linear UCB)

  • Contextual Bandit의 대표적인 알고리즘
  • 유저의 context xtx_t에 따라 reward를 선형 모델로 추정:
At=arg⁡max⁡a[xt,a⊤θ^a+αxt,a⊤Aa−1xt,a]A_t = \arg\max_a \left[ x_{t,a}^\top \hat{\theta}_a + \alpha \sqrt{x_{t,a}^\top A_a^{-1} x_{t,a}} \right]
  • θ^a\hat{\theta}_a: action a에 대한 파라미터
  • Aa=Da⊤Da+IA_a = D_a^\top D_a + I: action a의 관측된 context 누적
  • 즉, 같은 action이라도 user의 context가 다르면 다른 reward를 줄 수 있음

추천 시스템에서의 활용

online 학습이 가능하다.

  • 유저 cold-start: 개인화 정보 부족 시 다양한 arm 탐색
  • 아이템 cold-start: 신규 아이템에 traffic 유도
  • 실시간 반응 반영: 유저의 클릭/구매 여부에 따라 모델이 즉시 반응

유저 추천

  • 유저 수가 작고 아이템 수가 많은 상황
  • 후보 아이템 리스트 고정 → bandit은 후보 중 어떤 아이템을 노출할지 결정

유사 아이템 추천

  • 특정 아이템을 기준으로 유사 아이템을 추천
  • bandit은 노출 후 반응이 좋았던 아이템 조합을 강화 학습

Temporal and Sequential Models

유저의 선호는 고정된 것이 아님, '지금' 고객이 어떤 아이템을 선호할지 예측하는 것이 핵심

  • Temporal Dynamics의 중요성

    • 계절성, 주기성 등도 추천 품질에 영향을 줄 수 있음
    • 사용자 선호도 자체가 시간에 따라 변화

Long-Term Dynamics

Time Weight Collaborative Filtering

기존 item-based CF에 시간 정보를 가중치로 추가

기본 CF 방식:

r(u,i)=∑j∈Iu∖{i}Ru,j⋅Sim(i,j)∑j∈Iu∖{i}Sim(i,j)r(u, i) = \frac{\sum_{j \in I_u \setminus \{i\}} R_{u,j} \cdot Sim(i,j)}{\sum_{j \in I_u \setminus \{i\}} Sim(i,j)}

시간 반영 추가:

r(u,i)=∑j∈Iu∖{i}Ru,j⋅Sim(i,j)⋅f(tu,j)∑j∈Iu∖{i}Sim(i,j)⋅f(tu,j)r(u, i) = \frac{\sum_{j \in I_u \setminus \{i\}} R_{u,j} \cdot Sim(i,j) \cdot f(t_{u,j})}{\sum_{j \in I_u \setminus \{i\}} Sim(i,j) \cdot f(t_{u,j})} f(t)=e−λtf(t) = e^{-\lambda t}
  • 최근에 소비한 아이템일수록 높은 가중치를 부여
  • 오래된 행동은 덜 반영

Short-Term Dynamics

Session-based Recommendations with Graphs

Session-based Recommendation with Graph Neural Networks

  • 세션 단위로 사용자의 탐색 및 클릭 로그를 모델링
  • 사용자의 짧은 행동 흐름(검색, 클릭 등)을 반영하는 session-based 모델 필요

모델링 방식

  • 하나의 user는 여러 session을 가질 수 있음
  • session 안에서 item 간 edge 생성
  • 전체 그래프는 user, item, session 간 연결로 구성됨

관계 그래프 구성

  • ηu\eta_u: user와 item 간 long-term edge
  • ηs\eta_s: session과 item 간 short-term edge

Session context에 따라 user의 관심사 변화 학습 가능

Autoregression (자기회귀)

과거의 값을 이용해 미래 값을 예측하는 방식으로, 추천 시스템에서는 최근 행동을 기반으로 다음 행동을 예측할 수 있음.

이동평균 (Moving Average)

  • 최근 K개 값의 평균을 활용하여 예측

Simple Moving Average

y^t=1K∑i=1Kyt−i\hat{y}_t = \frac{1}{K} \sum_{i=1}^{K} y_{t-i}
  • K개의 최근 값을 단순 평균

Weighted Moving Average

  • 최근 값에 더 높은 가중치를 부여
y^t=∑i=1Kwiyt−i,∑wi=1\hat{y}_t = \sum_{i=1}^{K} w_i y_{t-i}, \quad \sum w_i = 1

Learning-based Moving Average

  • 각 시점별 weight를 학습을 통해 조정

더 일반화된 형태로 RNN, GRU, Transformer 기반 모델로 확장 가능

Factorized Personalized Markov Chains (FPMC)

**행렬 분해(Matrix Factorization, MF)**와 **마르코프 체인(Markov Chain, MC)**의 장점을 결합, 사용자의 장기적인 선호도와 단기적인 순차적 행동 패턴을 동시에 모델링

Factorizing personalized Markov chains for next-basket recommendation

  • 예측 함수: 사용자 u가 아이템 i를 구매할 확률 (또는 점수) x^u,t,i\hat{x}_{u,t,i}

    x^u,t,i=⟨Uu,Vi⟩+⟨Msu,t−1,Ni⟩\hat{x}_{u,t,i} = \langle U_u, V_i \rangle + \langle M{s_{u,t-1}}, N_i \rangle

    f(i∣u,j)=f(i∣u)+f(i∣j)+f(u,j)=γuU,I⋅γiI,U+γiI,J⋅γjJ,I+γuU,J⋅γjJ,Uf(i \mid u,j) = f(i \mid u) + f(i\mid j) + f(u,j) = \gamma_u^{U,I} \cdot \gamma_i^{I,U} + \gamma_i^{I,J}\cdot \gamma_j^{J,I} + \gamma_u^{U,J}\cdot \gamma_j^{J,U}

  • 목적 함수: BPR

    ∑(u,i,j)∈DS−ln⁡σ(x^u,t,i−x^u,t,j)+λ∣∣Θ∣∣2\sum_{(u, i, j) \in D_S} -\ln \sigma(\hat{x}{u,t,i} - \hat{x}{u,t,j}) + \lambda ||\Theta||^2

Personalized Ranking Metric Embedding (PRME)

거리 기반 유사도 측정

Personalized Ranking Metric Embedding for Next New POI Recommendation

PRME

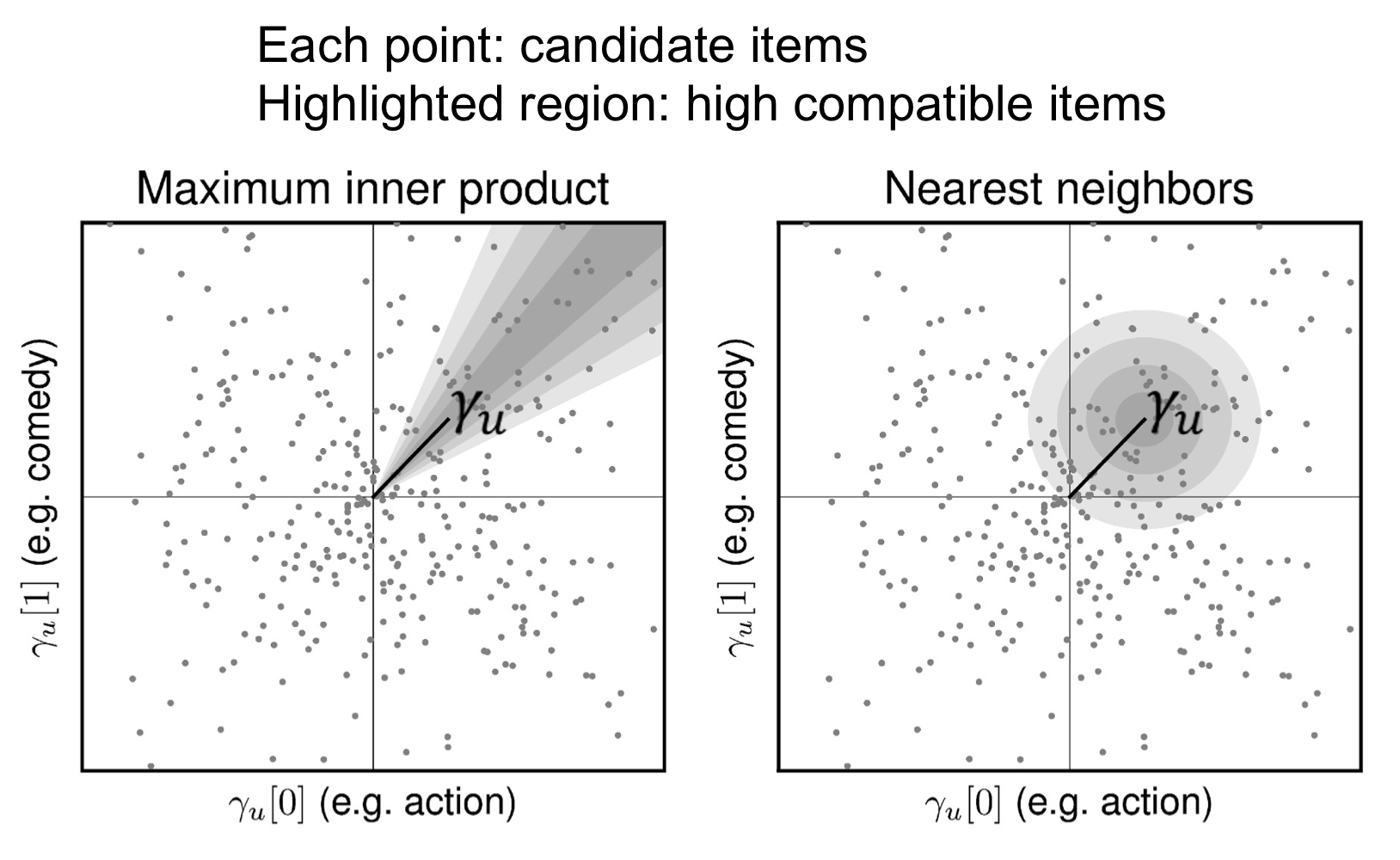
예측

σ(f(i∣u,j)−f(i−∣u,j))\sigma(f(i|u,j) - f(i^-|u,j))

f(i∣u,j)=−d(γu,γi)2−d(γi,γj)2=−∥γu−γi∥22−∥γi−γj∥22f(i \mid u,j) = -d(\gamma_u,\gamma_i)^2 - d(\gamma_i,\gamma_j)^2 = -\lVert \gamma_u - \gamma_i\rVert^2_2-\lVert \gamma_i - \gamma_j\rVert^2_2

GRU4Rec (2015)

세션 순서를 고려하여 다음에 클릭할 아이템을 예측하는 모델.
기존의 Matrix Factorization이나 Factorization Machine 기반 추천 방식이 세션의 순차성을 고려하지 못한다는 점을 극복함.

Session-based Recommendations with Recurrent Neural Networks

Session

  • 유저가 서비스를 이용하는 짧은 기간 동안의 행동 기록
  • 보통 클릭 로그나 페이지 방문 순서 등으로 구성됨

핵심 아이디어

  • Session sequence를 GRU 계열 RNN에 입력
  • 마지막 hidden state를 이용해 다음에 클릭할 아이템의 확률을 예측

모델 구조

  1. 각 아이템을 one-hot 또는 embedding vector로 변환
  2. GRU Layer를 통해 시퀀스를 처리
  3. 마지막 hidden state로 softmax 분포 계산

수식

  1. GRU transition:
ht=GRU(xt,ht−1)\mathbf{h}_t = \text{GRU}(\mathbf{x}_t, \mathbf{h}_{t-1})
  1. Softmax scoring:
y^t=softmax(Wo⋅ht+bo)\hat{y}_t = \text{softmax}(W_o \cdot \mathbf{h}_t + b_o)
  1. Loss (Ranking Loss - TOP1 loss 등):
L=∑(s,i+,i−)σ(y^i−−y^i+)+σ(y^i−2)L = \sum_{(s, i^+, i^-)} \sigma(\hat{y}_{i^-} - \hat{y}_{i^+}) + \sigma(\hat{y}_{i^-}^2)

학습 기법

  • 병렬 미니 배치 학습

    • Session 길이가 짧아 idle time이 많아질 수 있음
    • 여러 세션을 병렬적으로 묶어서 학습하는 구조 제안

  • Negative Sampling 전략

    • 아이템 수가 많아서 전부 학습하기 힘듦 → Negative Sampling
    • 인기 많은 아이템 위주 샘플링: 상호작용 없는 인기 아이템은 관심 없는 아이템이라고 가정

Neural Attentive Recommendation Machine (NARM)

user의 취향을 global level(GRU)과 local level(GRU + attention)로 분리

Neural Attentive Session-based Recommendation

모델 구조

Global Encoder: Sequential Behavior Modeling

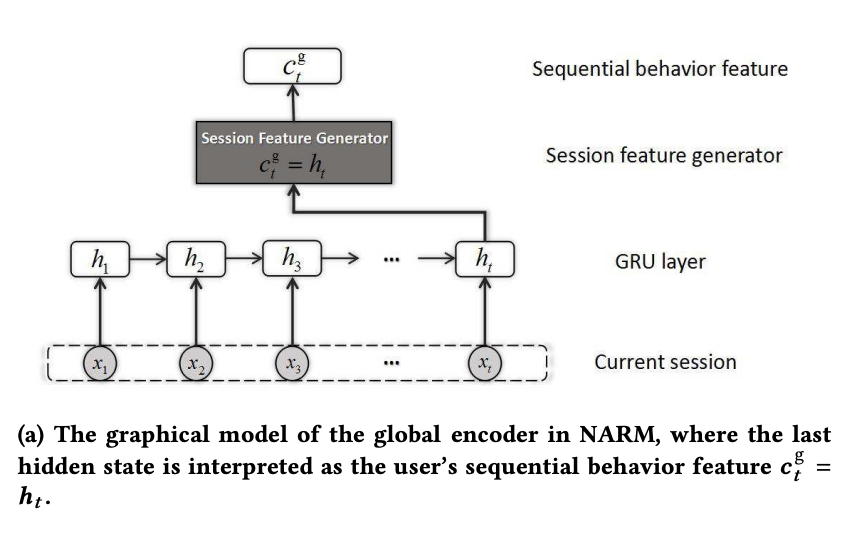
narm_global

각 state를 계산

ht=GRU(xt,ht−1)\mathbf{h}_t = \text{GRU}(\mathbf{x}_t, \mathbf{h}_{t-1})

세션의 전체 표현은 마지막 state로 정의

cg=hT\mathbf{c}_g = \mathbf{h}_T

Local Encoder: Attention-based Purpose Modeling

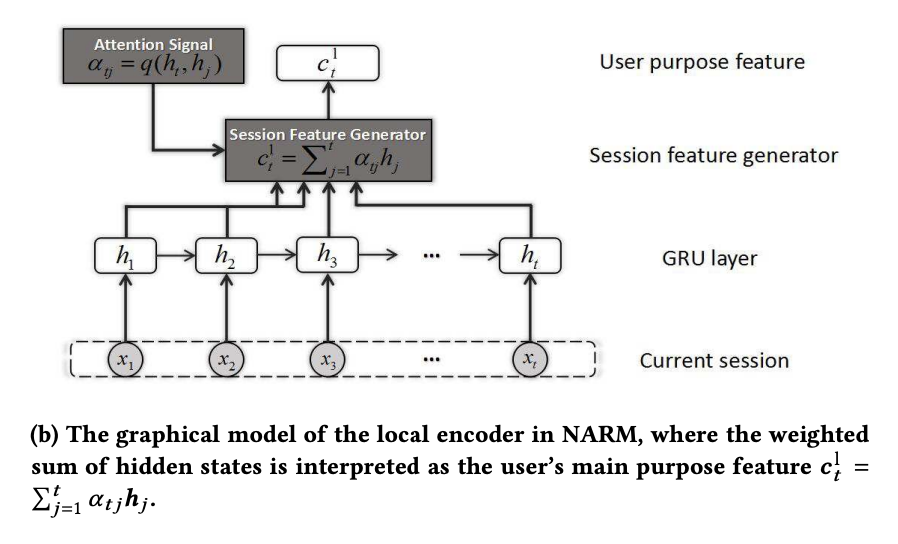
narm_local

각 시점의 attention score를 계산

et=q⊤⋅σ(W1hT+W2ht+b)e_t = \mathbf{q}^\top \cdot \sigma(\mathbf{W}_1 \mathbf{h}_T + \mathbf{W}_2 \mathbf{h}_t + \mathbf{b})

정규화

αt=exp⁡(et)∑k=1Texp⁡(ek)\alpha_t = \frac{\exp(e_t)}{\sum_{k=1}^{T} \exp(e_k)}

최종 local score

cl=∑t=1Tαtht\mathbf{c}_l = \sum_{t=1}^{T} \alpha_t \mathbf{h}_t

전체 구조

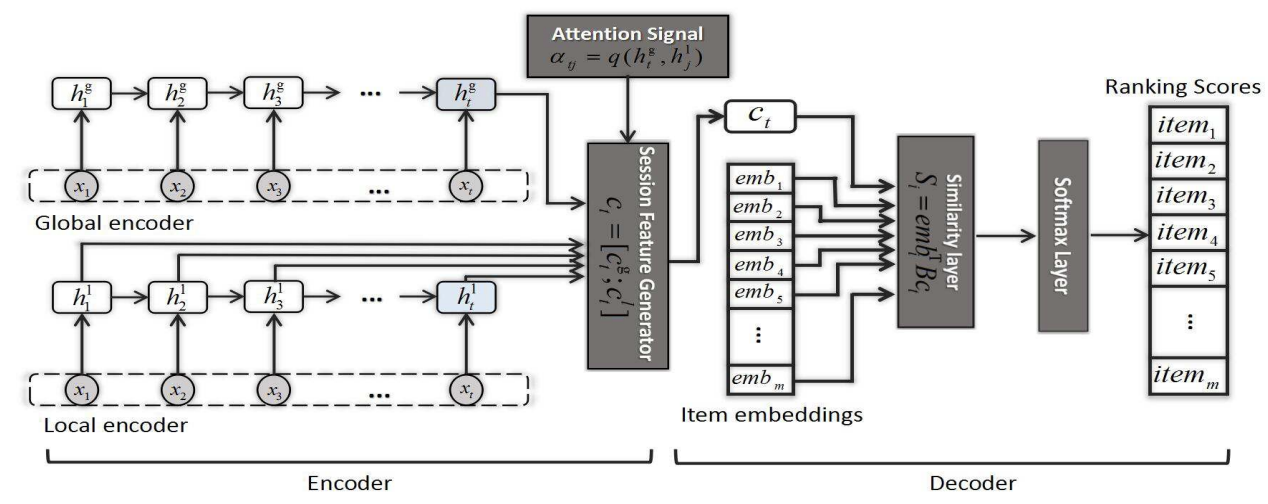
narm_final

SASRec

Self-Attentive Sequential Recommendation

Transformer 구조 기반의 시퀀스 추천 모델.
사용자의 과거 클릭 시퀀스를 기반으로 다음 아이템을 예측.

  • 구조
    • Transformer encoder 기반
    • item embedding + position embedding → self-attention
  • 특징
    • Dropout 적용 (embedding layer)
    • Input/output embedding 공유
    • Negative sampling + Binary cross entropy loss
  • 장점
    • RNN 기반 모델과 달리 병렬 처리 가능
    • 긴 시퀀스에도 효과적으로 학습 가능

수식

Loss=−∑su∈S∑t∈{1,…,n}[log⁡(σ(rot,t))+∑j∉sulog⁡(1−σ(rj,t))]Loss = - \sum_{s^u \in \mathcal{S}} \sum_{t \in \{1, \dots, n\}} \left[ \log(\sigma(r_{o_t, t})) + \sum_{j \notin s^u} \log(1 - \sigma(r_{j, t})) \right]
  • rot,tr_{o_t, t}: 시퀀스의 정답 아이템의 score
  • σ\sigma: 시그모이드 함수
  • j∉suj \notin s^u: negative sample로 사용되는 아이템

→ MC, RNN, CNN 기반의 기존 모델보다 병렬성과 정확도 측면에서 뛰어남

BERT4Rec

Bidirectional Encoder Representations from Transformers for RecSys

BERT 구조를 추천 시스템에 적용한 모델.
과거 + 미래 정보를 모두 활용하여 시퀀스 예측 정확도 향상.

  • 구조
    • Transformer encoder 기반
    • Masked item prediction 방식으로 학습
  • 특징
    • 양방향 self-attention 사용
    • Input/output embedding 공유
    • Cross-entropy loss 사용
  • 장점
    • 양방향 컨텍스트 활용
    • 다양한 위치 정보 학습에 유리

S3-Rec (Self-Supervised Learning for Sequential Recommendation with Mutual Information Maximization)

Self-Supervised Learning for Sequential Recommendation with Mutual Information Maximization

BERT4Rec 구조에 자기지도 학습을 결합한 모델.
Side information과 mutual information을 활용하여 더 강한 표현 학습 가능.

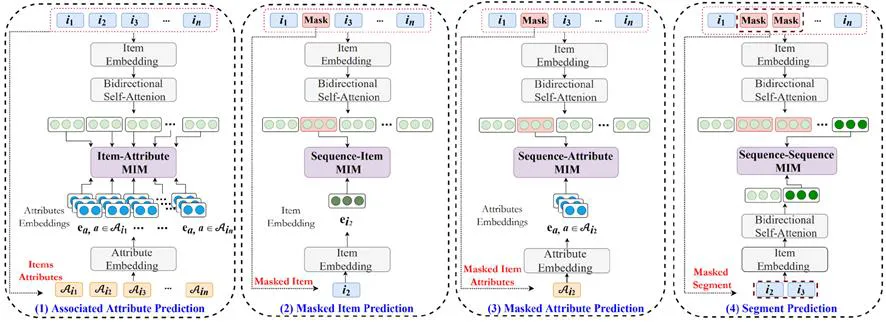
  • 구조 s3rec
    • BERT-like encoder + 4가지 auxiliary loss
  • 4가지 self-supervised task
    • Associated Attribute Prediction
    • Masked Item Prediction
    • Masked Attribute Prediction
    • Segment Prediction
  • 장점
    • Label 없이도 표현 학습 강화
    • 데이터 효율성 향상

CL4SRec (Contrastive Learning for Sequential Recommendation)

Contrastive Learning for Sequential Recommendation

시퀀스 추천에 contrastive learning 적용.
다양한 증강 기법을 통해 더 일반화된 시퀀스 표현 학습.

  • 구조
    • SASRec 기반 + contrastive loss 추가
  • augmentation 기법
    • item masking
    • cropping
    • reordering
  • loss
    • contrastive loss (positive pair는 유사하게, negative는 멀게)
  • 장점
    • label 없이 robust한 표현 학습
    • 적은 데이터에서도 성능 향상

수식

  • 전체 loss 함수:
Ltotal=Lmain+λLclL_{total} = L_{main} + \lambda L_{cl}
  • Main loss: 다음 아이템 예측을 위한 cross-entropy 기반 loss
Lmain(su,t)=−log⁡exp⁡(su,tTvt+1+)exp⁡(su,tTvt+1+)+∑vt+1−∈V−exp⁡(su,tTvt+1−)L_{main}(s_u, t) = -\log \frac{\exp(s_{u,t}^T v_{t+1}^+)}{\exp(s_{u,t}^T v_{t+1}^+) + \sum_{v_{t+1}^- \in V^-} \exp(s_{u,t}^T v_{t+1}^-)}
  • Contrastive loss: 같은 example의 augment끼리는 유사하게, 다른 example과는 구분되도록 학습
Lcl(suai,suaj)=−log⁡exp⁡(sim(suai,suaj))exp⁡(sim(suai,suaj))+∑s−∈S−exp⁡(sim(suai,s−))L_{cl}(s_u^{a_i}, s_u^{a_j}) = -\log \frac{\exp(\text{sim}(s_u^{a_i}, s_u^{a_j}))}{\exp(\text{sim}(s_u^{a_i}, s_u^{a_j})) + \sum_{s^- \in \mathcal{S}^-} \exp(\text{sim}(s_u^{a_i}, s^-))}
  • suai,suajs_u^{a_i}, s_u^{a_j}: 같은 example에서 파생된 augmentation
  • sim(⋅)\text{sim}(\cdot): cosine similarity 또는 inner product 기반 유사도
관련 글
Recsys Use cases
부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다. Recommender System Examples Youtube Deep Neural Networks for YouTube Recommendations > 1. Candidate Gene...
추천 시스템 정리 (2)
부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다. AutoEncoder for Recommender Systems 입력 데이터를 출력으로 복원하는 비지도 학습 모델. 중간 hidden layer는 input 데이터의 feature rep...
추천 시스템 정리 (1)
부스트캠프 AI Tech RecSys Track에서 학습한 강의들을 바탕으로 정리한 글입니다. Basic 유저는 직접 검색을 하지 않아도, 추천 알고리즘에 따라 유저의 취향에 맞는 아이템을 추천 받는다. (1) 유저의 직접적인 가이드가 없는 상황에서도 아이템을 선별해 주는 것과, ...